Opcje: Gamma – współczynnik szacujący zmianę ceny opcji

W poprzedniej części opisany został grecki współczynnik – delta. Pozwala on określić o ile zmienia się cena opcji w sytuacji zmiany ceny instrumentu bazowego. Jednak sama delta również zmienia się w zależności od ceny wykonania, zmienności czy czasu do wygaśnięcia opcji. Współczynnikiem greckim, który pozwala badać wrażliwość zmiany delty spowodowanej zmianą ceny instrumentu bazowego jest gamma. Jest to także jedna z tzw. „drugich pochodnych”. Gamma pozwala znacznie usprawnić zarządzanie strategią „delta-neutral” oraz dokładniej oszacować zmianę ceny opcji wraz ze zmianą wartości instrumentu bazowego.

PRZECZYTAJ KONIECZNIE: CZYM SĄ OPCJE? WPROWADZENIE

Czym jest współczynnik gamma

W najprostszej definicji, gamma określa jak szybko zmieni się delta opcji na skutek zmiany ceny akcji, indeksu czy waluty na której „oparta” jest opcja. Dzięki temu łatwiej oszacować zmianę ceny opcji. Oczywiście wielkość gammy nie jest stała. Z czego to wynika? Odpowiedź jest bardzo prosta. Delta opcji call może mieć wartość w przedziale 0 do 1, natomiast opcja put od 0 do -1. Skoro przedział jest skończony, a cena akcji czy indeksu teoretycznie może rosnąć w nieskończoność, to gamma musi się zmieniać. Istnieje kilka czynników, które mają wpływ na wielkość gammy. Są to:

• Cena rozliczenia opcji,
• Czas do wygaśnięcia opcji,
• Zmienność.

Cena rozliczenia opcji

Ten parametr ma wpływ na wielkość gammy. Z reguły opcje można podzielić na trzy rodzaje:

• opcje typu ITM,
• opcje typu ATM,
• opcje typu OTM.

Opcje ITM są inaczej nazywane „w pieniądzu”.  ITM oznacza typ opcji, które posiadają wartość wewnętrzną. W przypadku opcji call oznacza to, że cena wykonania opcji jest niższa od obecnej ceny rynkowej instrumentu bazowego. W przypadku opcji put cena wykonania opcji jest wyższa niż cena rynkowa instrumentu bazowego.

Opcje ATM to taki typ opcji, których cena wykonania jest równa obecnej cenie rynkowej instrumentu bazowego. Nie posiada wartości wewnętrznej. Na całą cenę opcji składa się tzw. wartość czasowa.

Opcje OTM są “najtańsze” pod względem nominalnym. Są to opcje, których cena wykonania jest albo wyższa od ceny rynkowej instrumentu bazowego (dla opcji call), lub niższa (dla opcji put).

Jak już wcześniej wspomniano, delta ma ograniczoną wartość od 0 do 1 w przypadku opcji call, oraz od 0 do -1 w przypadku opcji put. Dlaczego delta opcji call nie może być wyższa od 1? Odpowiedź jest prosta. Jeśli cena opcji call wzrosłaby o 1,5 w sytuacji, kiedy cena instrumentu bazowego wzrosłaby o 1, to pojawiłaby się możliwość arbitrażu. Polegałby on na tym, że inwestor wystawiłby opcję call i jednocześnie kupiłby odpowiednią ilość akcji.

Przykładowo:

Opcja call z ceną wykonania 50$ ma obecnie wartość 0,5$, a obecna cena akcji wynosi 50$. Przykładowo cena akcji wzrosłaby o 1$, a opcji o 1,5$. Oznaczałoby to, że delta opcji to 1,5 (wzrost instrumentu o 1$ powoduje wzrost delty o 1,5). Obecna cena opcji to 2$ z ceną wykonania 50$. Obecna cena rynkowa wynosi 51$. Inwestor wystawia opcję z ceną wykonania 50$ za 200$ (2$ * mnożnik). Inwestor wystawia opcję otrzymując 200$ i inwestuje 5100$ nabywając akcje (51$ * 100). Po pewnym czasie cena opcji spada poniżej 1$ (rynek znajduje nieefektywność). Inwestor odkupuje opcję i sprzedaje akcje po cenie 51$. Zysk z transakcji przekracza 100$.

Im bardziej opcja call jest ITM, tym ma większą deltę. Jednak zmiana delty powoli staje się coraz mniejsza wraz ze zbliżaniem się do 1. Oznacza to, że gamma opcji (zmiana delty) spada wraz ze zwiększaniem się delty. Jeśli wartość delty osiągnie poziom 1, to wartość gamma dla wzrostu wyniesie 0, natomiast w przypadku spadku ceny, gamma będzie miała zbliżoną wartość do 0.

Im bardziej opcja call jest OTM, tym ma mniejszą deltę. Granicą wartości delty jest 0. Oznacza to, że wraz ze spadkiem delty, zmiana jej jest coraz mniejsza. Oznacza to, że gamma opcji (zmiana delty), spada wraz ze zmniejszaniem się delty.

Jak nietrudno się domyślić, wartość gammy jest największa w okolicy ATM, czyli kiedy cena wykonania opcji jest najbliżej obecnej ceny rynkowej. Warto zaznaczyć, że wartość gammy jest zawsze dodatnia. Niezależnie czy opcja jest typu call, czy put. 

Warto posłużyć się przykładem. Poniżej znajdują się notowania opcji call i put na akcje Microsoft wygasające 18 marca 2022 roku. Poniższa grafika została wykonana 27 stycznia 2022 roku.

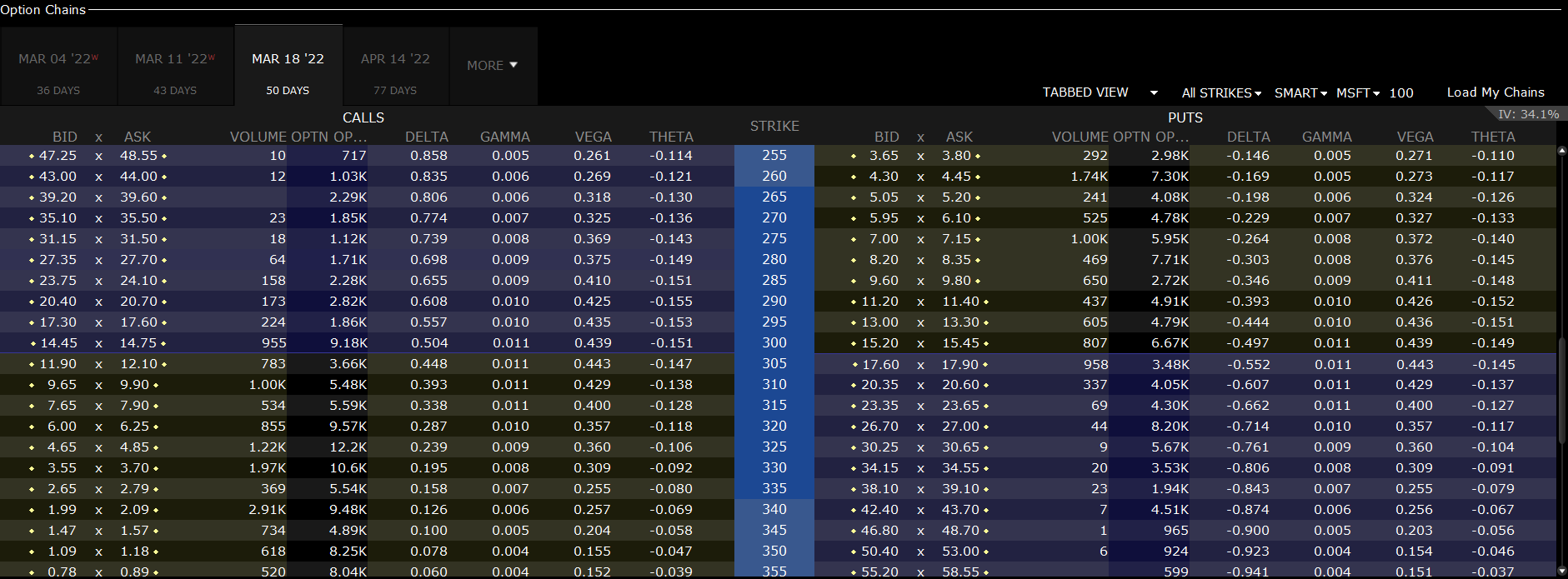
Źródło: platforma TWS

Na obrazie widać wyraźnie, że w przypadku opcji call gamma jest największa dla opcji znajdujących się ATM i spadają wraz z oddalaniem się od ceny rynkowej akcji Microsoft. Gamma dla opcji call z ceną wykonania 300% wynosi 0,011. Oznacza to, że zmiana ceny o 1$ powoduje zmianę delty o 0,011. Jak widać delta opcji call z ceną wykonania 300$ wynosi 0,504. Z kolei delta dla opcji call z ceną wykonania 295 wynosi 0,557. Szacując zmianę delty na podstawie gammy otrzymamy wartość 0,559. Oczywiście wyliczenie delty za pomocą gammy jest przybliżeniem, a nie dokładną wartością. Stąd też niewielka różnica w wyliczeniu „teoretycznej” i „rzeczywistej” delty.

Gamma i czas do wykonania opcji

Gamma ma związek z deltą, ta z kolei zależy również od czasu upływającego do wykonania opcji. Z tekstu o delcie wiemy, że im bliżej jest do wykonania opcji tym:

• Wzrasta wartość delty opcji ITM (w pieniądzu),
• Spada wartość delty opcji OTM (poza pieniądzem),
• Delta dla opcji ATM ma podobną wartość.

Poniżej przykładowe delty opcji dla opcji call na akcje Microsoft. Dane z 27 stycznia 2022 roku:

Z samą gammą dzieją się natomiast ciekawe zależności. W przypadku opcji będącej ATM wartość gammy rośnie. Ma to związek z tym, że im mniejszy jest czas do wygaśnięcia opcji, tym cena opcji będącej ATM jest bardziej wrażliwa na zmiany wartości instrumentu bazowego. 

Odwrotna sytuacja jest w przypadku opcji głęboko ITM oraz OTM. W przypadku opcji głęboko OTM (DOTM) z tygodniem do wygaśnięcia, szansa na to, że opcja stanie się ITM jest praktycznie zerowa. Z tego powodu, delta jest mało czuła na zmiany ceny instrumentu bazowego. Podobnie jest w przypadku opcji głęboko ITM (DITM). Jeśli delta jest powyżej 0,95, to gamma jest bardzo niewielka. Warto posłużyć się porównaniem gammy na podstawie opcji na akcje niemieckiej spółki technologicznej SAP SE. Cena jednej akcji wynosiła 4 lutego 2022 roku 110€.

Poniżej podsumowanie:

Jak widać dla opcji z najdłuższym czasem do wykonania gamma opcji staje się bardziej płaska. Wynika to z tego, że delty dla opcji DITM są znacznie mniejsze niż dla opcji o krótszym czasie do wykonania. Z kolei delty opcji DOTM dla opcji z dłuższym czasem do wykonania są wyższe niż delty opcji z tą samą ceną wykonania, ale z krótszym czasem do wygaśnięcia.

Dla porównania delty opcje na akcje SAP z 4 lutego 2022 roku:

Gamma a zmienność

W tej części opisana zostanie zależność między zmiennością, a gammą. W przypadku opcji na akcje spółek o niskiej zmienności delta opcji będących „lekko” ITM gwałtownie reaguje na zmianę ceny. Wynika to z tego, że handlujący opcjami nie spodziewają się dużej zmienności na akcjach z tego powodu nie płacą dużo za premię czasową. Z kolei dla opcji głęboko ITM oraz OTM niska zmienność opcji powoduje, że gamma drastycznie spada. W przypadku opcji DOTM (głęboko poza pieniądzem) powodem jest bardzo niska delta, w przypadku opcji DITM (głęboko w pieniądzu) powodem niskiej gammy jest bardzo wysoka delta. 

Zupełnie inaczej sytuacja wygląda w przypadku opcji na instrumenty mające bardzo dużą zmienność. W takiej sytuacji, gwałtowne zmiany ceny instrumentu bazowego nie są niczym niezwykłym. Powoduje to, że inwestorzy są skłonni zapłacić więcej za tego typu opcje nawet jeśli są głęboko poza pieniądzem. Powoduje to, że wartość czasowa opcji rośnie. Jednocześnie wysokie oczekiwania co do dużej zmienności powodują, że gamma jest stosunkowo „płaska”. 

Strategia delta – gamma neutralna

Delta może być także wykorzystywana do tworzenia strategii zabezpieczających portfel. Ta strategia polega na zbudowaniu portfela ze współczynnikiem delta na poziomie zero (tzw. delta neutral). W takiej sytuacji strata z portfela akcji jest rekompensowana zyskiem z opcji. Należy jednak zaznaczyć, że portfel w pozycji delta neutral znajduje się tylko przez krótką chwilę. Powodem jest ciągła zmiana delty opcji, przez co należy dokonywać korekty portfela (tzw. rebalancing). Okresowa zmiana portfela oznacza, że stosowana jest tak zwana dynamiczna strategia zabezpieczająca (dynamic delta hedging).

Jak widać stosowanie samej strategii delta neutralnej nie jest zbyt użyteczne w przypadku dużych wahań na rynku. Powodem jest „gamma”, która zmienia współczynniki delta opcji co powoduje „niedopasowanie” delt pozycji. Rozwiązaniem jest takie zbudowanie portfela, aby współczynnik delta oraz gamma były neutralne. 

Przykładowo:

Inwestor kupuje 10 opcji call na akcje SAP z ceną wykonania 110€ wygasającą 18 marca 2022 roku. Delta takiej opcji wynosi 0,481. Oznacza to deltę na poziomie 481 (0,481 * 10 * mnożnik). Cena jednej opcji wynosi 344€ (3,44€ * mnożnik). Aby zneutralizować wpływ delty inwestor musi sprzedać 481 akcji spółki SAP po 110€. W efekcie, delta wynosi 0. Jednak jedna opcja call posiada 0,044 gammy. Pomnożono przez 1000 akcji wynosi 44. Aby zmniejszyć gammę inwestor postanowił wystawić 40 opcji sprzedaży z ceną wykonania 126€. Gamma jednej opcji wynosi 0,011. Pomnożone przez 4000 akcji, gamma wynosi -44. W efekcie, gamma wynosi 0. Jednak delta wystawionej opcji wynosi 0,954 (wystawiona opcja put ma dodatnią deltę). W efekcie, delta pozycji wynosi 3816. Warto dodać, że jedna opcja ma wartość 1715€ (17,15€ * mnożnik). W wyniku tych obliczeń inwestor powinien sprzedać krótko 3816 akcji SAP po cenie 110€. W efekcie, portfel posiada zarówno neutralną gammę, jak i deltę. 

Podsumowanie

Gamma opcji jest bardzo istotnym współczynnikiem greckim. Pozwala oszacować, jak zmieni się wartość gammy w sytuacji zmiany ceny instrumentu bazowego. Dzięki temu inwestor potrafi „przewidzieć” jak może zmienić się delta, co pozwala dokładniej oszacować potencjalny zysk z transakcji na opcjach. Kolejnym zastosowaniem gammy jest budowa portfela, który jest delta-gamma neutral. 

Czy wiesz, że…?

Saxo Bank jest jednym z nielicznych brokerów Forex, posiadającym w swojej ofercie opcje waniliowe. Inwestor ma do dyspozycji łącznie ponad 1200 opcji (waluty, akcje, indeksy, stopy procentowe, surowce). SPRAWDŹ